В школе учат инвариантности геометрических углов для треугольников и четырехугольников. Само наличие инвариантности ценно в той части, что определяет вместе со свободой поведение системы. Ограничения (инварианты) и свобода некоторых переменных в геометрии даны как свойства, например:
Основные свойства треугольников. В любом треугольнике:
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
В частности, все углы в равностороннем треугольнике равны.
3. Сумма углов треугольника равна 180 º .
Из двух последних свойств следует, что каждый угол в равностороннем
треугольнике равен 60 º.
4. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний
угол BCD. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним: BCD = A + B.
5. Любая сторона треугольника меньше суммы двух других сторон и больше
их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).
.
Но школа не учит онтологии, где существуют конструктивные инварианты в отношении субстанций линейной геометрии; расстояния (пассивное) и угла (активное). Покажем простым и наглядным методом индукции, что существует закон сохранения субстанции. Для расстояния он как бы очевиден, а вот для угла не совсем.
Представим, что у нас в руках проволока определенной длины.
а) Пусть мы изготовляем равносторонний (для простоты) треугольник (внутренние углы -180°). Тогда угол конструктивного изгиба (извне) равен 120° + 120° + 120° = 360°.
б) Пусть мы делаем квадрат, тогда угол конструктивного изгиба (извне) равен 90°+90°+90°+90° = 360°.
в) Пусть мы изготовляем пятиугольник. Угол конструктивного изгиба (извне) равен 5*72°=360°.
Какой бы мы многоугольник не стоили, нам проволоку «по кругу» всегда надо будет изогнуть на 360 градусов. Таким образом, мы можем сделать вывод:
Конструктивная сумма углов любого плоского выпуклого многоугольника:
равна 360°.
Можно напомнить, что существует «Теорема о сумме углов многоугольника»:
Сумма [внутренних] углов n-угольника равна 180°(n − 2).
***
Казалось бы, а для чего это нужно в онтологии (устройстве мира)?
- во-первых, это очень познавательно, хотя бы в части того, с какой (буквально!) точки зрения смотреть на систему: изнутри или снаружи. Здесь намекается на некоторые эффекты поведения спинов элементарных частиц.
- во-вторых, можно заметить, что внешний «образ» и внутренний совпадают, при n=4. То есть – в случае четырехугольника. Не говорит ли это о том, что подмеченная «квадратичность» всех эйдосов как-то онтологически связаны с данным фактом?
- в-третьих, зная, что в эйдосе линейной геометрии:
точка – линия – угол – плоская фигура – объемная фигура,
лосевское становление обеспечивается углом, а плоская фигура (в части построения) относится к будущему (ее мы только и можем формировать из наличных субстанций) есть надежда лучше понять экономические законы, используя гомологию.
.
Примечание.
1. Если говорить о гомологии, то бензол – это свернутый «шестиугольник», обладающий запасом энергии.
*****
Дополнительно, пояснительный рисунок из статьи «Онтология. Экономика. Природа рынка«:
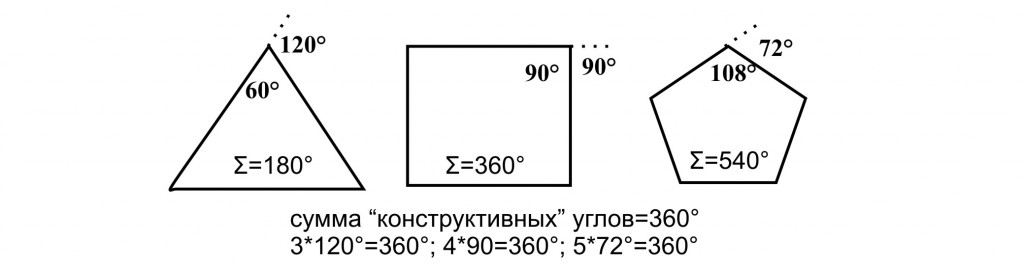Рисунок показывает, что «конструктивный инвариант» внешних углов остается постоянным.