Уважаемые коллеги по сайту АТ недавно опубликовали статьи, где трактуется закон единства и борьбы противоположностей (ЗЕБП) в отношении золотого сечения (ЗС):
Шенягин В.П.Закон единства и борьбы противоположностей в математических терминах золотых констант и монады
Шенягин В.П.Закон единства противоположностей в живой разумной природе: гипотеза
Белянин В.С. Заметки в защиту закона единства и борьбы противоположностей и немного о прочем
Василенко С.Л. Благосклонная ремарка к полемике о формализованной иллюстрации принципа единства и взаимодействия противоположностей
Никитин А.В. О философском споре математиков …
.
Я, естественно, данный закон не признаю, в силу отсутствия в нем самой диалектики как принципа глобального конструктивного движения (он символизирует скорее «ступор»). А золотое сечение вижу как определенный статус (этап) в онтологическом «каркасе» эйдоса, где он соответствует онтологической структурности.
Дарвин, со своими положениями о роли изменчивости и постоянстве в эволюционном движении был гораздо ближе к диалектике чем этот закон ЗЕБП.
.
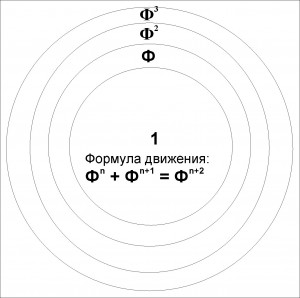
Не привлекает меня тот момент, что более всего за ЗС видят обычно «отрезки». В то время как по эйдетическому четвертому статусу он отражает «площади». То есть, я полагаю, что его символом должны служить «площадь». В частности площадь последующего круга равна площади двух предыдущих.
Исходная мысль этих положений была дана в статье «Организационные свойства эйдоса (гармония, эмерджентность)» , где был показан смысл выражения в эйдосе:
Х + 1 = X2
.
По своему статусу в эйдосе эта формула циклична, что позволяет реализовать известную рекурсию:
Фn + Фn+1 = Фn+2
{Хорошим подтверждением тому служат треугольники Кеплера, которые тоже поддерживают рекурсию площадей:
Василенко С.Л. Фибоначчиевый ряд золотых треугольников Кеплера // АТ. – М.: Эл. № 77-6567, публ. 22546, 26.09.2016. – URL: http://www.trinitas.ru/rus/doc/0016/001e/00163062.htm }
Само эйдетическое представление констант дано в («Метод как экспликация логики»):
i – 1 – π/2 – Ф – е (2),
Если опираться на тезис А.Ф. Лосева, что диалектика это «логос об эйдосе«, то в стиле Дарвина математическим константам можно дать следующую диалектическую характеристику в виде принципов организации:
1) изменчивости, движения (i) ;
2) постоянства, устойчивости (1) ;
3) цикличности, повторяемости (π/2);
4) изоморфизма, самоподобия (Ф);
5) гомологии, композиционности (е);
***
а) Все эти принципы поддерживаются ортогональностью и кумулятивностью (мнимая «вертикаль», действительная «горизонталь», единичный круг который ортогонален в своем движении этим двум осям, наращивание площадей с «нормой» движения Ф, спираль движения площадей…);
б) Нельзя забывать в рамках онтологии, что число – идеализированная форма бескачественного полагания (по Лосеву). Только в этом варианте возможно «безразмерное» сложение 1 + Ф = Ф2 в эйдосе. В физике нельзя сложить импульс и силу, получив энергию. Поэтому, одно дело математические интерпретации, другое дело онтология (устройство мира). Эйдос »отвечает» именно за онтологию мира. А математические константы – это частный случай…
в) Вспоминая Ч. Дарвина, нельзя не отметить, что вся сравнительная биология после него развивалась «под знаменем» гомологии (гомотопии, …). И все пять принципов, ИМХО, красиво ложатся в эволюционную теорию…
Шенягин В.П.Закон единства и борьбы противоположностей в математических терминах золотых констант и монады
Шенягин В.П.Закон единства противоположностей в живой разумной природе: гипотеза
Белянин В.С. Заметки в защиту закона единства и борьбы противоположностей и немного о прочем
С.Л. Василенко Благосклонная ремарка к полемике о формализованной иллюстрации принципа единства и взаимодействия противоположностей
Никитин А.В. О философском споре математиков …
Я, естественно, данный закон не признаю, в силу отсутствия к нему достаточной импирики. А золотое сечение вижу как определенный статус (этап) в онтологическом «каркасе» эйдоса, где он соответствует дарвинисткому принципу преемственности постоянства и изменчивости в эйдосе математических констант. В соответствии с правилами эйдоса, второй статус есть сущность («нечто постоянное при любом изменении»).
Постоянство отражает сохранность сущности, а изменчивость – ортогональность в развитии. Если за исходность возьмем наличие мнимого числа (i), то изменчивость требует ортогональности действительного числа, где единица – сущность числа, заключающая в себе как мнимость (акт полагания, движение)), так и фиксированность (знака).
Круг, проведенный в такой системе координат, есть изменчивость реальной единицы в комплексной плоскости. А траектория движения единицы ортогональна к мнимой и действительной осям. Если единица Единого, понимаемая субстанально как единство пассивной и активной субстанции (П/А) есть сущность, то мерой изменчивости круга, движения по нему будет величина π/4.
Следующий этап развития это движение площадей. Здесь в статье «Организационные свойства эйдоса (гармония, эмерджентность)» был показан смысл выражения:
Х + 1 = Х2.
Это смысл движение круговых (вложенных) площадей, где сумма предыдущих двух последовательно вложенных площади, равны общей площади. Диалектика (преемственности) здесь сохраняет эволюционные предыдущие накопления. Константа Ф – это величина трансформации от круга площадью Ф, к добавлению единичной площади (1) к новой площади Ф2.
Графический принцип диалектического движения на 4-ом статусе («Метод как экспликация логики»): Фn + Фn+1 = Фn+2
Уважаемые коллеги (по корпусу диалектики) недавно опубликовали статьи, где трактуется закон единства и борьбы противоположностей:
Шенягин В.П.Закон единства и борьбы противоположностей в математических терминах золотых констант и монады
Шенягин В.П.Закон единства противоположностей в живой разумной природе: гипотеза
Белянин В.С. Заметки в защиту закона единства и борьбы противоположностей и немного о прочем
С.Л. Василенко Благосклонная ремарка к полемике о формализованной иллюстрации принципа единства и взаимодействия противоположностей
Никитин А.В. О философском споре математиков …
Я, естественно, данный закон не признаю, в силу отсутствия к нему достаточной импирики. А золотое сечение вижу как определенный статус (этап) в онтологическом «каркасе» эйдоса, где он соответствует дарвинисткому принципу преемственности постоянства и изменчивости в эйдосе математических констант. В соответствии с правилами эйдоса, второй статус есть сущность («нечто постоянное при любом изменении»).
Постоянство отражает сохранность сущности, а изменчивость – ортогональность в развитии. Если за исходность возьмем наличие мнимого числа (i), то изменчивость требует ортогональности действительного числа, где единица – сущность числа, заключающая в себе как мнимость (акт полагания, движение)), так и фиксированность (знака).
Круг, проведенный в такой системе координат, есть изменчивость реальной единицы в комплексной плоскости. А траектория движения единицы ортогональна к мнимой и действительной осям. Если единица Единого, понимаемая субстанально как единство пассивной и активной субстанции (П/А) есть сущность, то мерой изменчивости круга, движения по нему будет величина π/4.
Следующий этап развития это движение площадей. Здесь в статье «Организационные свойства эйдоса (гармония, эмерджентность)» был показан смысл выражения:
Х + 1 = Х2.
Это смысл движение круговых (вложенных) площадей, где сумма предыдущих двух последовательно вложенных площади, равны общей площади. Диалектика (преемственности) здесь сохраняет эволюционные предыдущие накопления. Константа Ф – это величина трансформации от круга площадью Ф, к добавлению единичной площади (1) к новой площади Ф2.
Графический принцип диалектического движения на 4-ом статусе («Метод как экспликация логики»): Фn + Фn+1 = Фn+2


Комментарии В. Сахно поддерживаю. Для «Закона ЗЕБП» используются только две «противоположные» величины и условная интерпретация их восприятия, а противоположностей на самом бывает деле много-много! Полагаю, что величины Х и У можно считать противоположными, если произведение Х * У = 0, где Х и У могут быть представлены в виде числовых матриц! Это уже настоящие противоположности, вплоть до ИХ тождества, когда Х = У и Х * Х = 0